이 글은 골든래빗 <코딩 테스트 합격자되기 파이썬편>의 11장 써머리입니다.
[그래프 기본 개념]: 노드(vertex)와 간선(edge)를 이용한 비선형 데이터 구조. + 가중치도 있음
간선: 간선의 방향유무에 따라 directed graph(방향 그래프), undirected graph(무방향 그래프)
가중치: 가중치 유무에 따라 weight graph(가중치 그래프)
순환: 순환 여부에 따라 cycle graph(순환 그래프), acyclic graph(비순환 그래프)
[그래프 구현 방식]: 표현 방법은 어느 하나가 뛰어나지 않고 장단점이 있다.) adjacency matrix(인접 행렬),
1) adjacency matrix(인접 행렬): 2차원 배열로 표현하기
ex) 해당 값에는 가중치를 넣는다. 0->1이 400인 경우, (0,1) = 400이 된다.
시간복잡도가 O(1)로 좋음. 2->93의 값을 확인할려면 (0,2) 확인하면 됨. (노드 데이터가 문자면, 문자열을 숫자로 매핑함)
구현 난이도도 낮음
단, 간선 수가 적은 경우 공간복잡도 낭비할 수도 있다는 단점 有
코딩 테스트에서 노드 개수가 1000개 미만이라면 인접 행렬이 편의적으로 좋다.
2) adjacency list(인접 리스트): 배열 구조 (정점 v, 가중치 w, 다음 노드 next) 구조로 관리
여기서 리스트의 인덱스가 가 시작 노드이고 v는 도착 노드가 된다.
모든 노드에 간선이 연결된 경우를 제외하면 메모리를 절약할 수 있다는 장점이 있음
[그래프 탐색]
1) DFS(depth-first search): 최대 깊이로 이동하며 차례대로 방문 후, 방문할 노드 없으면 최근 노드로 돌아가 방문 노드 여부 확인 (back tracking 연관)
최단 경로 문제가 아니라면 DFS를 고려한다. 경로마다 특징을 저장해야할 때 DFS 사용(BFS는 경로 특징 저장 불가)
<스택을 이용한 구현>
stack 비었음? -> 비었으면 모든 노드 방문 -> 탐색 종료
stack 안비었음! -> 노드 pop(= 최근 stack에 push한 node)
해당 pop된 노드 방문 여부 확인 (미방문시 방문 처리) : 즉, stack에서 pop하면서 방문 처리
방문한 노드와 인접한 모든 노드 확인, 미방문 노드 stack에 push
<재귀 함수 이용한 구현>
dfs(N): N번 노드를 방문 처리하고 N번 노드와 인접한 노드 중 아직 미방문 노드를 탐색
2) BFS(breadth-first search): 시작 노드와 가장 가까운 노드 우선 방문
가중치가 없는 그래프에서 최단 경로 보장
<큐를 이용한 구현>
queue 비었음? -> 비었으면 종료(모두 방문)
queue 안비었음? -> queue에서 node pop. -> 해당 팝된 노드와 인접한 모든 node 확인 -> 미방문 node push 및 방문처리
[Dijkstra 다익스트라 = 데이크스트라]: 가중치 有인 그래프의 최단 경로 구하기 (단, 음의 가중치가 없어야 可) 성능 우수함
원리: greedy(탐욕법); 최소 비용(가중치) 우선 선택.
시간복잡도: O(V^2). 우선 순위 큐로 개선 시, O(ElogV)
구현 방법:
시작 노드 설정, 시작노드 - 특정 노드까지 최소 비용 저장 공간, 직전 노드 저장 공간 설정
최소 비용, 직전 노드 저장 공간 = INF로 초기화.
시작 노드 최소 비용 = 0. 직전 노드 = 자기 자신
미방문 노드 중, 최소 비용이 가장 적은 노드 선택
현재까지 구한 최소 비용 & 각 노드까지 가는 최소 비용 비교하여 작은 값 갱신 & 직전 노드 갱신
노드 개수에서 1을 뺸 만큼 이 과정 반복
01단계 시작 노드 A의 최소 비용은 0, 직전 노드는 A로 초기화

02단계 미방문 노드 중 최소 비용 노드 A를 선택. 이때 최소 비용이 갱신된 노드의 직전 노드를 A로 갱신.

03단계 미방문 노드 중 최소 비용 E를 선택. 선택한 E를 거쳤을 때 최소 비용을 갱신여부 확인(비교). C 최소 비용은 4, E를 거쳤을 때 1+2=3 이므로 C의 최소 비용을 3, 직전 노드를 E로 수정.

04단계 미방문 노드 중 최소 비용 C 선택. 선택한 C를 거쳤을 때 최소 비용을 갱신여부 확인(비교). 노드 D의 경우 기존 최소 비용이 INF(경로가 없음)이지만, D를 방문하는 방법이 C를 거치면 C의 최소 비용(3) + C → D의 가중치(8)를 합쳐 11이 되어 더 작으므로 최소 비용을 11로, 직전 노드를 C로 갱신.
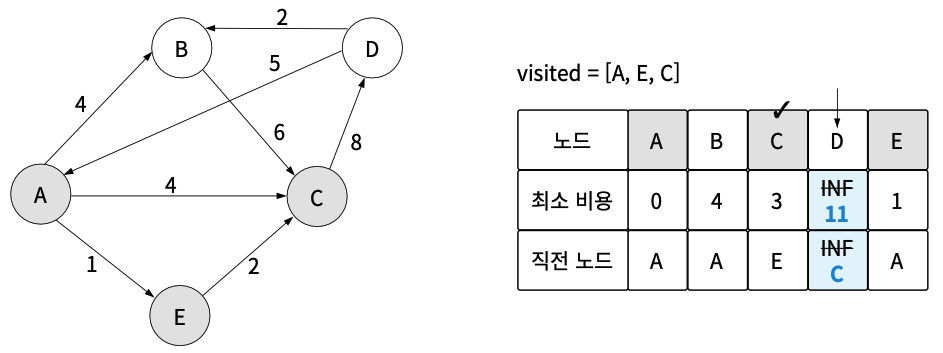
05단계 미방문 노드 중 최소 비용 B 선택. 선택한 B를 거쳤을 때 최소 비용 갱신 여부 확인하지만 현 상태에서는 없으므로 갱신도 없다.

06단계 미방문 노드 중 최소 비용 D 방문. D를 거칠 때 최소 비용 갱신 여부 확인하지만 미방문 노드 없으므로 끝.

07단계 전부 방문한 이 상태에서 만들어진 표는 각 노드의 최솟값 경로 정보를 담고 있다.


[bellman-ford 벨만-포드]: 매 단계마다 모든 간선 가중치 재확인으로 최소비용 계산 -> 음의 가중치 그래프도 可
단, 음의 순환은 불가능. 음의 순환 감지만 可 (음의 순환은 최단경로 구하기 불가능함)
시간복잡도: O(VE) ~ O(V^3)
01단계 우선 시작 노드를 A로 정하고 최소 비용을 0, 직전 노드를 A, 나머지 노드는 INF로 초기화한다.

02단계 노드 A에서 A를 거쳐 각 노드 B, C, D, E까지 바로 직행하는 비용에 대해 기본값 INF보다 적은 값이 있다면 갱신. 이때 해당 정점의 최소 비용은 최소_비용(A)(숫자), 가중치가 있는 간선은 간선(A, B)(숫자)로 표시. 간선이 없는 경우는 INF로 계산.
※ A에서 A를 거친다 = A가 시작 노드. A에서 시작하면 A를 거치는 것
- 최소_비용(A)(0) == 최소_비용(A)(0) + 간선(A, A)(0) : 불변
- 최소_비용(B)(INF) > 최소_비용(A)(0) + 간선(A, B)(4) : 최소_비용(B)를 INF에서 4로 갱신
- 최소_비용(C)(INF) > 최소_비용(A)(0) + 간선(A, C)(3) : 최소_비용(C)를 INF에서 3으로 갱신
- 최소_비용(D)(INF) == 최소_비용(A)(0) + 간선(A, D)(INF) : 불변(A -> D 간선 없음)
- 최소_비용(E)(INF) > 최소_비용(A)(0) + 간선(A, E)(-6) : 최소_비용(E)을 -6으로 갱신

03단계 A -> B를 거친 후 나머지 노드에 가는 경우를 생각해보자
- 최소_비용(A)(0) < 최소_비용(B)(4) + 간선(B, A)(INF) : 불변 (B->A 없음)
- 최소_비용(B)(4) == 최소_비용(B)(4) + 간선(B, B)(0) : 불변
- 최소_비용(C)(3) < 최소_비용(B)(4) + 간선(B, C)(INF) : 갱신하지 않음 (B->C 없음)
- 최소_비용(D)(INF) > 최소_비용(B)(4) + 간선(B, D)(5) : 9로 갱신 (A->B->D)
- 최소_비용(E)(-6) < 최소_비용(B)(4) + 간선(B, E)(-6) : 갱신하지 않음 (B->E 없음)

04단계 A -> C를 거친 후 나머지 노드에 가는 경우를 생각해보자.
- 최소_비용(A)(0) < 최소_비용(C)(3) + 간선(C, A)(INF) : 불변 (C->A 없음)
- 최소_비용(B)(4) < 최소_비용(C)(3) + 간선(C, B)(2) : 불변 (A->C->B값이 최솟값이 아님)
- 최소_비용(C)(3) == 최소_비용(C)(3) + 간선(C, C)(0) : 불변
- 최소_비용(D)(9) < 최소_비용(C)(3) + 간선(C, D)(INF) : 불변 (C->D 없음)
- 최소_비용(E)(-6) < 최소_비용(C)(3) + 간선(C, E)(INF) : 불변 (C->E 없음)
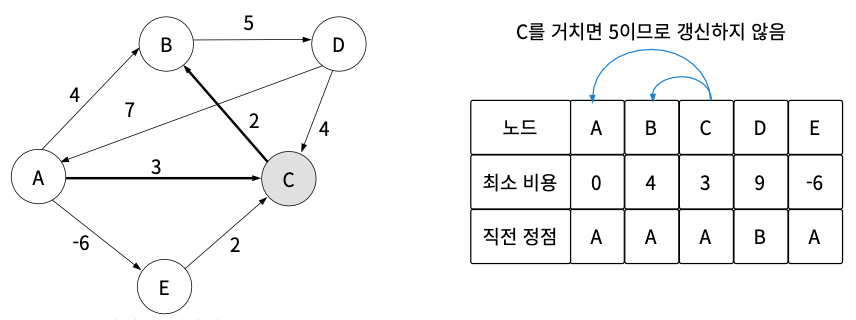
05단계 A -> D를 거친 후 나머지 노드에 가는 경우는 존재하지 않는다. (A->D 없음)
06단계 A -> E를 거친 후 나머지 노드에 가는 경우를 생각해보자. 이 때, 모든 최단 경로에 대해 노드의 최소 비용을 체크했으므로, 벨만-포드 알고리즘의 첫 번째 반복이 끝났다.
- 최소_비용(A)(0) < 최소_비용(E)(-6) + 간선(E, A)(INF) : 불변 (E->A 없음)
- 최소_비용(B)(4) < 최소_비용(E)(-6) + 간선(E, B)(2) : 불변 (E->B 없음)
- 최소_비용(C)(3) == 최소_비용(E)(-6) + 간선(E, C)(0) : -4로 갱신 (A->E->C가 더 최솟값)
- 최소_비용(D)(9) < 최소_비용(E)(-6) + 간선(E, D)(INF) : 불변 (E->D 없음)
- 최소_비용(E)(-6) < 최소_비용(E)(-6) + 간선(E, E)(INF) : 불변

07단계 이게 첫 번째 반복이 끝났다. 이 알고리즘은 ‘노드 개수 – 1’번 반복, 여기선 01단계 01단계~06단계 06단계를 4번 더 반복한다.

08단계 2번째 반복을 시작한다. 노드 A에서 A를 거쳐 각 노드까지 가는 비용을 갱신합니다. 첫 번째 과정과 마찬가지 과정을 반복하면서 추가 갱신이 있을 때 이를 반영한다.
- 최소_비용(A)(0) == 최소_비용(A)(0) + 간선(A, A)(0) : 불변
- 최소_비용(B)(4) == 최소_비용(A)(0) + 간선(A, B)(4) : 불변
- 최소_비용(C)(-4) < 최소_비용(A)(0) + 간선(A, C)(3) : 불변
- 최소_비용(D)(9) > 최소_비용(A)(0) + 간선(A, D)(INF) : 불변
- 최소_비용(E)(-6) == 최소_비용(A)(0) + 간선(A, E)(-6) : 불변
왜 정점 개수 -1만큼 반복? <- 매 연산마다 최단 경로가 1개씩 확정됨!

N-1반복보다 많다 = 음의 순환 有
최단 경로의 간선 개수는 최대 N – 1이므로 이 이상이 있다면 음의 순환이 있다는 의미.

음의 순환에 빠지는 건 벨만-포드 알고리즘의 한계다?
흔히 벨만-포드의 알고리즘의 한계점으로 ‘음의 순환이 있을 때 최단 경로를 구하지 못한다’를 자주 말합니다. 이 말을 듣고 ‘벨만-포드 알고리즘은 음의 순환이 있을 때 최단 경로를 구하지 못하는 좋지 못한 녀석’이라고 오해하기 쉬운데 그렇게만 이해하면 안 됩니다.
사실 엄밀히 말하면 그래프에 음의 순환이 있으면 어떤 알고리즘도 최단 경로를 구할 수 없습니다. 다만 음의 가중치를 다루는 최단 경로 알고리즘은 음의 순환에 빠질 수 있는 것이죠. 다시 말해 벨만-포드 알고리즘은 음의 가중치가 있는 그래프에서 최단 경로를 찾을 수 있는 대신 음의 순환에 빠질 수 있고, 다익스트라 알고리즘은 음의 가중치가 있는 그래프에서 동작하지 못하므로 아예 언급되지 않는 것입니다.

그러니 음의 순환에 빠지는 벨만-포드 알고리즘의 특징을 알고리즘의 한계로 보면 안 됩니다. 오히려 음의 순환을 감지할 수 있는 것이죠.
[floyd-warshell 플로이드-워셜]: 각 노드부터 나머지 노드까지의 최단 경로 모두 구하는 것. (출제 빈도 낮음)
문제 38) 깊이 우선 탐색 순회
깊이 우선 탐색으로 모든 그래프의 노드를 순회하는 함수 solution( )을 작성하세요. 시작 노드는 start로 주어집니다. graph는 [출발 노드, 도착 노드] 쌍들이 들어 있는 리스트입니다. 반환값은 그래프의 시작 노드부터 모든 노드를 깊이 우선 탐색으로 진행한 순서대로 노드가 저장된 리스트입니다.
제약 조건
- 노드의 최대 개수는 100개를 넘지 않습니다.
- 시작 노드부터 시작해서 모든 노드를 방문할 수 있는 경로가 항상 있습니다.
- 그래프의 노드는 문자열입니다.
입출력의 예

입출력 예를 보면 [출발 노드, 도착 노드]의 쌍이 리스트로 들어옵니다. 첫 번째 graph를 그림으로 표현하면 다음과 같습니다.

문제 39) 너비 우선 탐색 순회
너비 우선 탐색으로 모든 노드를 순회하는 함수 solution( )을 작성하세요. 시작 노드는 매개변수 start로 주어집니다. graph는 (출발 노드, 도착 노드) 쌍들이 들어 있는 리스트입니다. 반환값은 그래프의 시작 노드부터 모든 노드를 너비 우선 탐색으로 진행한 순서대로 노드가 저장된 리스트입니다.
제약 조건
- 노드의 최대 개수는 100개입니다.
- 시작 노드부터 시작해서 모든 노드를 방문할 수 있는 경로가 항상 있습니다.
- 그래프의 노드는 숫자입니다.
입출력의 예

문제 40) 다익스트라 알고리즘
주어진 그래프와 시작 노드를 이용하여 다익스트라 알고리즘을 구현하는 solution( ) 함수를 작성하세요. 인수는 graph, start 총 2개입니다. graph는 딕셔너리로 주어지며 노드의 연결 정보와 가중치가 저장되어 있습니다. 예를 들어 {‘A’: {‘B’: 2, ‘C’: 5}}이면 A는 B, C에 각각 가중치 2, 5로 연결되어 있는 것입니다. start는 문자열로 주어지며 출발 노드를 의미합니다. 반환값은 시작 노드부터, 각 노드까지 최소 비용과 최단 경로를 포함한 리스트입니다.
제약 조건
- 그래프의 노드 개수는 최대 10,000개입니다.
- 각 노드는 0 이상의 정수로 표현합니다.
- 모든 가중치는 0 이상의 정수이며 10,000을 넘지 않습니다.
입출력의 예

예를 들어 첫 번째 입력에 대한 결과를 그림으로 나타내면 다음과 같습니다. 반환값을 분석하면 시작 노드를 기준으로 B의 최소 비용은 4이고, 최단 경로는 A → C → B입니다.

문제 41) 벨만-포드 알고리즘
벨만-포드 알고리즘을 구현한 solution( ) 함수를 구현하세요. graph의 각 데이터는 리스트입니다. 첫 번째 데이터는 0번 노드 기준으로 연결된 노드 정보, 두 번째 데이터는 1번 노드 기준으로 연결된 노드 정보입니다. 노드 정보의 구성은 (노드, 가중치)와 같습니다. source는 시작 노드입니다. 반환값은 최단 거리를 담은 distance 리스트와 최단 거리와 함께 관리할 직전 노드 predecessor를 리스트에 차례대로 담아서 [distance, predecessor] 형식으로 반환하면 됩니다. predecessor에서 시작 노드는 None으로 표시합니다. 만약 음의 가중치 순회가 있다면 [-1]을 반환하세요. 음의 가중치 순회란 순환하면 할수록 가중치의 합이 적어지는 순회를 말합니다.
제약 조건
- 노드의 최대 개수는 100개입니다.
- 각 간선의 가중치는 -100 이상 100 이하입니다.
입출력의 예

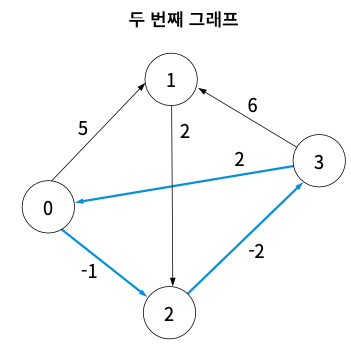
예를 들어 입력에 있는 그래프는 다음과 같습니다.
두 번째 그래프의 경우 음의 가중치 순회가 존재하므로, [-1]이 반환된 것을 알 수 있습니다.

문제 42) 게임 맵 최단 거리
https://school.programmers.co.kr/learn/courses/30/lessons/1844
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 풀이 미완성
문제 43) 네트워크
https://school.programmers.co.kr/learn/courses/30/lessons/43162
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 풀이 미완성
문제 44) 배달
https://school.programmers.co.kr/learn/courses/30/lessons/12978
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 풀이 미완성
문제 45) 경주로 건설 (2020 카카오 인턴)
https://school.programmers.co.kr/learn/courses/30/lessons/67259
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 풀이 미완성
문제 46) 전력망을 둘로 나누기
https://school.programmers.co.kr/learn/courses/30/lessons/86971
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 풀이 미완성
추천 문제 1) 가장 먼 노드
https://school.programmers.co.kr/learn/courses/30/lessons/49189
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 풀이 미완성
추천 문제 2) 방의 개수
https://school.programmers.co.kr/learn/courses/30/lessons/49190
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 풀이 미완성
추천 문제 3) 순위
https://school.programmers.co.kr/learn/courses/30/lessons/49191
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 풀이 미완성
추천 문제 4) 합승 택시 요금 (카카오 2021)
https://school.programmers.co.kr/learn/courses/30/lessons/72413
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 풀이 미완성
추천 문제 5) 타겟 넘버
https://school.programmers.co.kr/learn/courses/30/lessons/43165
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 풀이 미완성
추천 문제 6) 여행 경로
https://school.programmers.co.kr/learn/courses/30/lessons/43164
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 풀이 미완성
'TechStudy > CodingTest' 카테고리의 다른 글
| chp16 그리디 (Greedy) (0) | 2024.03.02 |
|---|---|
| chp10 집합(set) (0) | 2024.01.06 |
| chp9 트리(tree) (4) | 2023.12.21 |
| chp8 해시(hash) (1) | 2023.12.13 |
| chp6 스택(Stack), chp7 큐(Queue) (4) | 2023.12.07 |



