ITF: Interpretable Time Series
FM: feature manipulation
<개요 2023.11.02>
기존 합성데이터 생성 문제점: black box에서 만들어졌기에 해석이 어려움
-> 시계열 연속함수 기반 두 가지 해석 기법 제시:
1) ITF-FM: deep autoencoder(=AE) 조정
2) ITF-GAN: 적대적 학습 (GAN) 사용
-> 해석 가능한 고품질 합성데이터 생성

$N_{head}$: 추가 노이즈 패턴에 의한 corrupted output 추정
[1] ITF-FM
일반적인 생성은 총 4단계로 진행된다.
1단계: ITF-AE를 주어진 데이터 안에서 훈련한다. (confident data reconstruction이 필요함)
2단계: network 가중치 $\theta$들은 고정(frozen)한다. 그리고 for $\forall$ samples $X$ in a given dataset $\Sigma =[X_{1},...,X_{j},...,X_{J}]$, encoded feature $z$ are collected in $Z=[z_{1}, ... , z_{j}, ... , z_{J}]$ where $z_{j}=[z_{1,j}, ... , z_{i,j}, ... , z_{I,j}]^{T}$ and $j \in \mathbb{N}$ in $[1,J]$.
3단계: $Z$를 따라서 매 $i$번째 원소에 대해 확률 분포 $P_{i}(z_{i,:})$를 추정한다.
훈련이 끝나면, 얻은 분포와 파라미터 조정에 따라서 new sample $X'$가 생성된다. 이에 대한 $Z'$의 정의는
$Z'=Z+\gamma \times \beta \circ s\times \sigma _{n}^{T}$
where a scaling factor $\gamma \in \mathbb{R}$, an attention vector $\beta \in {0,1}$ of length $I$,
and a Gaussian sampled noise vector $\sigma _{n}$ ~ $N(0,1)$ of length $J$.
표준편차 $s=[s_{1}, ... , s_{i}, ... , s_{I}]^{T}$ where 샘플 $j$에대한 확률 분포 $s_{i}=Var(z_{i,:})^{0.5}$
attention vector $\beta$: feature가 조정되었는지 여부를 조절
scaling factor $\gamma$를 늘리거나 latent space $Z'$의 features들 더욱 조절: $\Sigma'$ 에서 diverse distribution
4단계: decoding 공식으로 $X'$ in $Z'$을 도출한다.

그리고 extracted noise features $z_{\sigma}$와 noise pattern $P_{\sigma}$를 기반으로 noise를 resample한다.
( $N_{head}$로 추정된 파라미터 특성들로 이뤄진 분포를 샘플링해서 noise 생성)
noise 수준은 noise 분포 파라미터나 $\gamma$로 조절.
여기까지가 일반적인 단계 진행이고 본문에 적용된 알고리즘 방식은 이러하다.

-> noise pattern $P_{\sigma}$과 조작된 features $Z'$가 샘플을 $\Sigma'$ 에서 생성
-> 이 데이터는 무제한으로 만들 수 있으며, 비슷한 특성을 지니고 해석이 가능.
$Z'$ 공식은 scaling factor $\gamma$, an attention vector $\beta$로 network가 추정하지 못하는 통계적 파라미터 결정
(reparameterization trick과의 큰 차이점)
[2] ITF-GAN
input: $x$ ~ $N(0,1)$ for $T$ samples.
GAN을 통해 feature $z'$ 추정
-> decoder equation이 series $X'$ 를 reassemble
-> $N_{head}$는 $X'$에 noise pattern 추가
-> reconstruct $Y_{\sigma}$없이 multi headed 신경망의 output은 생성된 sample $X'$
-> discriminator(2개의 LSTM으로 구성됨)가 원본과 생성된 series를 구분. (사실 아무 신경망으로 구성할 수 있다.)
-> 단일 결과물을 sigmoid activation 함수로 scaling
[3] ITF-encoding
다변수 시계열 인코딩은 Bag of Functions(BoF) 접근 방법에 기반한다. 그러나 본문은 이 접근 방식에 추가로 확장된 부분이 있다.
(arithmetic operator $z_{0}$, multi-head encoding에 조건부 input, decomposed signal의 remainder에서 노이즈 패턴 추정)
제안하는 autoencoder 구조는 아래의 그림과 같다.

backbone: X의 feature extraction
-> 3가지 head에 전달
F head는 연속 함수를 선택하고 O head는 선택된 함수들간의 관계를 정하며, P head는 파라미터 추정을 한다.
-> 여기서 나온 z가 decoder에 전달
-> Y로 합쳐짐
[backbone $\mathfrak{B}$]
MLP (multi-layer perceptron)로 구성 (MLP말고 다른 구성도 가능함)
목적: $X$를 연속성과 조건형 정보를 포함한 임베딩 벡터 $\xi \in \mathbb{R}^{T}$로 인코딩
-> 함수, arithmetic operators, 파라미터 로 분해
output $=\xi = \mathfrak{B}_{\theta}(X)$ (* the learnable parameters = $\theta$ of $\mathfrak{B}$)
첫 레이어는 4T input으로, 두 번째 레이어는 2T로, 세 번째는 T로 줄여나감.
이 layer 사이에 batch normalization(BN), rectified linear unit(ReLU) 활성화 함수 사용.
[Function head $\mathfrak{F}_{head}$]

목표 output: a selective soft distribution 샘플 $z_{f}\quad s.t. \;\; \forall z_{f} \in [0,1] \subset \mathbb{R} $
where for $\forall$ function proposal $f$ in the collection $F$.

레이어 사이에 BN, ReLU가 사용됨, output에 sigmoid로 0, 1 사이로 sacling
$\theta$를 $\mathfrak{F}_{head}$ network의 파라미터라고 할 때, selective score $z_{f}$ 추정 식은 다음과 같다:
$$z_{f}= \frac{1}{1 + e ^{- (\mathcal{F}_{\text{head}, \theta}(\xi))}} $$
(sigmoid기반 함수)
[Operator head $\mathfrak{O}_{head}$]

구성물: 자체 MLP, sigomid, hardlim layer(이진분류 활성화함수: 입력 x이 0이상이면 1, 0미만이면 0을 출력, but 역전파에 사용 어려움)

input: the concatenation $\xi$(backbone features), $z_{f}$(selected functions)
output = discrete selection $z_{0} \in {0,1}$
여기서 hardlim 활성화함수는 0.5를 기준으로 operator를 설정한다.

gradient 계산도 직관적으로 기초 연산인 더하기 빼기로 하였다.
단, Mathematical operator 선택으로 인해 exploding or vanishing outputs이 되지 않도록 유의한다.
[Parameter head $\mathfrak{P}_{head}$]

다른 head의 추정에 따라 최대 자유도를 가능케 함. 1st layer후에 BN, 2nd layer후에 ReLU 사용.
input: the concatenation of backbone 정보, 함수, operators($\xi\frown z_{f} \frown z_{0}$)
output: $N$개의 함수 후보에서 함수 파라미터 $z_{p} \in \mathbb{R}^{N} \quad s.t. \;\; \forall z_{p} \in [b,c] \subset \mathbb{R} $
3rd layer에는 시그모이드 활성화함수와 [b,c] 범위의 대응하는 함수 파라미터로 묵는다.
ex) sine wave $a_{3}$은 $b_{3}=0$과 $c_{3}=\pi$ 사이에에서 clipped된다.

[Decoder $D$]

$D$ 는 시계열 $Y$를 재조립한다.
1) the selection score $z_{f}$는 operators $z^{0}_{0}=1$인 $z_{0}$에 곱해진다.
2) selected 함수에 파라미터가 삽입되면 output는 the horizion $T$에서 계산된다.
3) 결과값: output trajectory $Y(t)$ where $t=[0,1,...,T-1]$ is 벡터 길이

[Residual stacking]
성능 최적화를 위해 $K$개의 다중 AE(Auto-encoder) 구조를 순차적 스택형태로 저장함. 즉, $K$개의 ITF-AE를 stack함.
1st AE input = the input trajectory $X$ = $X_{0}$ (* $Y_{0}=0$)
AE input 일반화: $X_{k}=X_{k-1}-Y_{k-1}$
다음 AE의 input = the residual between the output and the previous output
last AE(stack) output = residual $Y_{k} = D_{k}(\xi_{k}(X_{k-1}-Y_{k-1}))$
output $Y=\sum_{n=1}^KY_{k}=X_{0}-X_{K}$ = input - the final remainder
이는 $\forall$ latent features $Z=[z_{1}, z_{2}, ... , z_{K}]$가 위 decoder 식 $y(t)$와 결합된 것이다.
이러한 계산 방식의 효과: 컴퓨터 자원 사용 감소, 추가 assembling 과정 생략(displaced) 가능
[Noise head]

stacked AE의 마지막 remainder $X_{K}$ = 데이터 noise, 복제될 수 없는 요인
-> decoded 신호 위에 조절 가능한 noise를 포함하는 과정을 도입 -> $X_{K}$가 $N_{head}$로 입력됨
$N_{head}$: 인공 noise 생성을 위한 특정 패턴의 noise 파라미터를 추정한 것
-> $N_{head}$는 2개의 선형 레이어 $s_{\sigma}$와 $\mu_{\sigma}$로 현 noise 패턴 $P_{\sigma}$ 추정
-> $T$값을 위해 아래 3가지 noise 패턴 방법들 중 하나를 통해서 샘플화. 즉, 선택된 확률분포 샘플링으로 noise 생성
-> noise 분포 추정부터 noise 수준의 최대 최소를 설정할 수 있음.
3가지 noise 패턴 샘플링 방법:
1) 확률밀도함수(PDF): white noise $p_{n}$ 정규분포 ($\mu$: 평균, $s$: 표준편차)
$$ p_n(x_i) = \frac{1}{s \sqrt{2 \pi}} e^{-\frac{1}{2} \left( \frac{x_i - \mu}{s} \right)^2} $$
2) PDF가 평균 주변에서 동일한 환경에서의 균등 noise 패턴 $p_{u}$
$$ \begin{equation} p_u(x_i) = \begin{cases} \frac{1}{b - a} & \text{if } a \leq x_i \leq b \\ 0 & \text{otherwise} \end{cases} \end{equation}, \quad \mu = \frac{a + b}{2}, \quad s^2 = \frac{(b - a)^2}{12} $$
3) 상관계수 파라미터 $0 \le r \le 1$로 정규분포 패턴 $n$에서 red noise 생성하는 방법
$$x_1 = n(x_1), \quad x_i = r x_1 + (1 - r^2)^{0.5} n(x_{i + 1}), \quad i \le 1$$
noise 추가된 output $Y_{\sigma}= \sigma + Y$
이 과정을 통해 원본 데이터는 함수, 연산자(operator), 매개변수(파라미터), 그리고 매개변수화된 noise 모델로 변환
-> 인위적인 noise로 재구성되어 수정된 data로 만들어진 출력물 = 합성데이터!!
[Learning]
목표: 경사하강법으로 $X$와 $Y_{\sigma}$ 사이의 MSE loss 최소화
모든 층의 가중치 θ: 한 번의 학습 단계에서 최적화
$K$ latent spaces와 bags (=collection) $F$의 연결에서 loss의 정의는 아래의 식으로 정의
$\min_{\theta} \mathcal{L}_{\text{MSE}}(X, Y_{\sigma}) = \frac{1}{T} \sum_{t=0}^{T-1} (x_t - y_{\sigma,t})^2=\frac{1}{T} \sum_{t=0}^{T-1} \left(x_t - P_{\sigma}(t, z_{\sigma}) - \sum_{j=1}^{K\cdot N} z_{\sigma}^{j-1} \cdot z_f^j \cdot F^j(t, z_p^j)\right)^2$
문제점: MSE loss만 사용시, noise = 0이 됨 ($s_{\sigma}\rightarrow0$). 즉, $Y$와 noisy 신호 $Y_{\sigma}$ 불균형 문제
-> scaling factor $0 \le \alpha \le 1$ 를 계산식 및 2번째 loss term에 도입.
* 2번째 term: 예측된 $s_{\sigma}$와 타겟 표준편차$s_{t}$ 사이의 거리 규제
-> 이에 따른 손실(loss)값 계산식은 아래와 같이 변경
$\mathcal{L} = \alpha \cdot \mathcal{L}_{\text{MSE}}(X, Y_{\sigma}) + (1 - \alpha) \cdot \mathcal{L}_{\text{MSE}}(s_{\sigma}, s_t)$
[4] 실험
ITF-FM(scaling 파라미터 $\gamma$ ), ITF-GAN(타겟 noise 표준편차 $s_{t}$)을 여러 기준과 데이터셋으로 ablation studies 진행
ITF-FM: $\gamma = 1.5$, 파라미터 $z_{p}$만 조작.
환경: Nvidia Quadro RTX 5000
최적화 방법: ADAM
batch, learning rate를 다양하게하여 10번 시도중 최고 결과만 선택
합성 sine wave 데이터셋에 대해 feature 조작과 적대적 network(이진 교차 엔트로피 손실, BCELoss) 로 조사
사용한 데이터: 독일 에너지 소비산업 데이터, Microsoft 주식 거래 데이터
평가 대분류 : 1) 데이터 질에 대해 통계적인 측정 및 평가, 2) 작업에 대한 수치적 성능에 대한 평가
[평가 기준 1]: 품질에 대한 통계적 평가
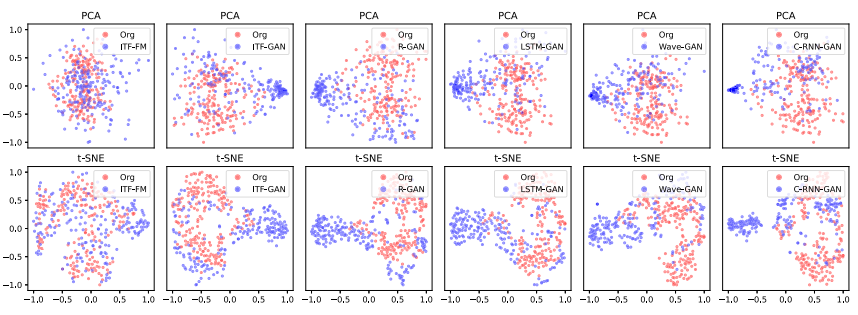
주성분 분석(PCA, Principal Component Analysis), 확률적 t분포 임베딩 (t-SNE, stochastic neighbor embedding) 사용

- 딥러닝 등의 중간 Layer의 Output Feature 들은 대체적으로 고차원의 영역의 데이터이다. 이러한 데이터들은 직관적으로 이해하기가 어렵기 때문에, 저차원으로 시각화하여 Visualization을 진행하는데, t-SNE가 자주 사용된다.
- PCA(주성분 분석)과 차원축소의 개념에서는 비슷하지만, 목적과 방식이 달라, 혼용해서 보완 사용하기도 한다.
시각적 평가(visual evaluation): 기존 데이터와 합성 데이터 비교로 수행
𝛴 와 𝛴 ' 거리를 MSE로 측정 -> 적은 거리 = 두 데이터가 유사함, 먼 거리 = 두 데이터가 완전 다름
통계적 상관관계 측정 방법 3가지 사용
1) 단기 시계열 거리 (STS): 시계열의 상대적 진폭 변화로 형태 유사성 측정 . 0에 가까운 점수는 유사함을 의미
2) 피어슨 상관계수(Pearson correlation): 목표 범위 0.3 ~ 0.8. 단, 1은 금지; 1은 원본 데이터의 복사본 = 부적절한 합성데이터
3) 헬린저 거리 (HD, Hellinger Distance ): 유클리드 노름(norm)으로 데이터 분포 유사성 측정
가우시안 커널 밀도 추정을 통해 확률 분포 계산 -> 0에 가까움(데이터 간 유사도 높음)을 목표. 단 0은 아님
* 1에 가까움: 데이터 간 큰 차이
[평가 기준 2]: 정량적 분석
합성 데이터와 원본 데이터에 대한 하위 작업
-> 2MLP(다층 퍼셉트론)로 판별적(discriminative) 및 예측적(predictive) 점수 산출
판별적 점수: 원본 데이터와 합성 데이터 구분, 분류
ex) 낮은 분류 오류 = 합성 데이터와 원본 데이터의 구분이 어려움
예측적 점수: 합성 데이터의 시간 역학(dynamic) 학습으로 원본 데이터의 다음 단계 예측
-> "Train on Synthetic, Test on Real" (TSTR) 접근법 사용 및 MAE로 예측 점수 평가
[실험 방법]: 다양한 도메인(오디오, 의료) 사용에 다양한 방법(RNN, LSTM에서 합성곱)으로 비교
1) R(recurrent)-GAN: 다차원의 의료 시계열 데이터 생성을 위해 사용
input: 반복(recurrent) layer -> 조건부 input이 있으면 input이 연결됨
2) LSTM-GAN: 2개의 100 cell이 있는 stack LSTM layer 사용. 두 레이어 output에는 dense layer 있음.
입력 차원은 판별기와 생성기의 추가 선형층으로 보장됨.
3) Wave-GAN: 1차원 합성곱 기반으로 오디오 wave를 합성
input: 6개의 transposed 합성곱, a dense later
판별기는 5개의 합성곱 기반
4) C(Continuous)-RNN-GNN: 판별기의 양방향 LSTM과 생성기의 LSTM의 조합
LSTM output: fully connected layer 적용
클래식 음악 데이터에 적용
[Sine wave 결과]
실험 설정: 10,000개의 시퀀스 샘플 생성, 균일 샘플된 함수 파라미터 사용,
3개 sine waves, Gaussian noise 포함 각 시퀀스 100개 값 구성
진폭: [0.1, 1], frequency: [0.005, 0.2], 주기(phase): [0, 2π]
ITF-FM 실험 단계:
ITF-AE를 훈련 subset으로 학습 -> reconstruction 평가 -> 해석 가능한 latent 특성을 균등 분포로 수정
-> 조절한 특성을 decoder에 넣어 샘플 생성 및 평가

ITF-AE: 낮은 MSE 손실로 수렴 -> 구별 불가능한 패턴의 유사한 분포 생성
ITF-FM: 대부분의 기준에서 최고 점수 달성
R-GAN: 최고의 판별(Disc) 점수
ITF-GAN: 최고의 예측(Pred) 점수
Wave-GAN: 가장 낮은 성능
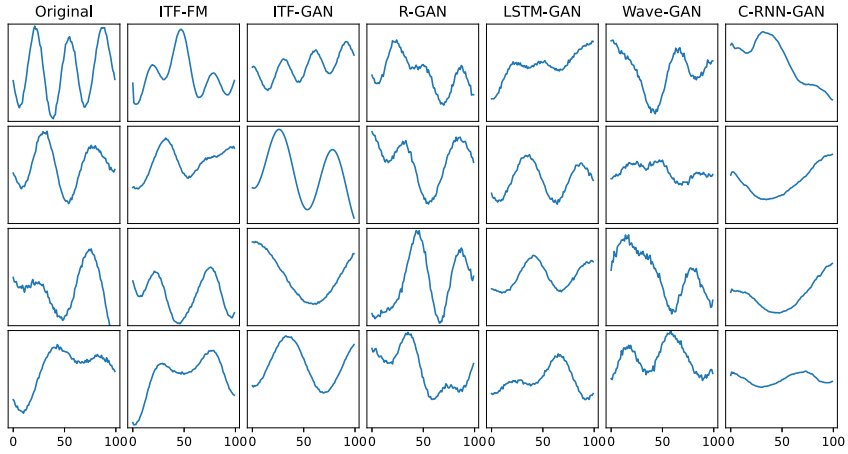
C-RNN-GAN 을 제외하고 모든 방법이 신뢰할 만한 합성 샘플 생성
ITF-FM: 원본 데이터의 기본 구성 요소를 합성 데이터에 포함
ITF-GAN: 출력이 함수 구성 요소와 파라미터로 설명 가능 -> 모델이 deterministic output series 전달
(다른 GAN 방법들은 예측 불가능한 블랙박스)

방법간 큰 차이는 없는 양상. but ITF-GAN과 C-RNN-GAN이 소규모 군집 형성 양상을 보임. ITF-FM는 단일 분포 느낌
-> 원본데이터를 커버하지도못하는 C-RNN-GAN (t-SNE)를 제외하고 전반적으로 좋은 결과
[산업 데이터 결과]: 산업용 에너지 데이터, Microsoft 주식 데이터 기반 실험
PU (Public Utility) 데이터: 독일 가구의 에너지 소비 데이터 (2년간 15분 간격으로 수집됨)
-> 12시간(48개 길이의 중첩 윈도우)로 전처리
MS (Microsoft Stock) 데이터: 1986~2023년 매일 갱신된 데이터.
-> 시퀀스 길이 0-1 사이로 스케일링, 추가 length를 다루기위해 T = 70으로 설정
-> 시간에 따른 급격한 변화를 줄이고 상대적 변화로 변형

두 AE 모델 모두 데이터 주요 특성 포착 -> 낮은 MSE 점수
PU 데이터>>
예측 점수: ITF-FM, ITF-GAN 최고 성능
판별 점수: ITF와 Wave-GAN이 판별 GAN 점수에서 우수
MS 데이터셋>>
Wave-GAN, LSTM-GAN, C-RNN-GAN은 낮은 판별 점수 어려움 (드문드문한 데이터 특성 때문)
ITF-GAN이 예측 점수에서 다른 GAN 방법들보다 우수. 그러나 판별 점수는 R-GAN이 조금 더 좋음


두 데이터셋 모두 R-GAN, LSTM-GAN, Wave-GAN은 원본 샘플에 비해 noise가 더 많아보이게 나옴

PU 데이터셋>> 모든 방법이 특정 패턴에서만 분포 외 샘플 생성
ITF-FM이 가장 우수한 질적 결과
C-RNN-GAN을 제외한 다른 방법들은 분포 fitting에서 유사한 성능
MS 데이터셋>> ITF-GAN, R-GAN, LSTM-GAN이 원본과 유사한 분포 생성
C-RNN-GAN과 Wave-GAN은 모드 붕괴(mode collabs*)로 인해 쉽게 구별 가능한 샘플 생성
* the mode collabs: 생성기가 다양한 데이터를 생성하는 대신 몇 가지 특정한 모드(패턴)에 집중하여 반복적으로 동일하거나 유사한 샘플을 생성하는 현상
[Ablation study]: 전체 다 있는 상태에서 수행한 것과 거기서 하나 뺀 고 수행한 것을 비교하는 것
ITM-FM 결과는 ITF-AE 성능에 편향됨 -> feature 조정 수준 $\gamma$ 에 대한 ablation study 시행
* $\gamma$↑ = 조정된 feature의 noise ↑ -> 다양성 증가

방법: $\gamma$를 0.3부터 2.7까지 0.6 단위로 증가시키며 평가
MSE, STS, 피어슨, Hellinger: $\gamma$ 상승하면 같이 상승 -> 신호, 분포간 거리 증가 의미
$\gamma=0$ -> AE 성능을 의미
pred는 큰 변화없이 일정한 양상 -> 데이터가 더욱 더 분산(scattering)되어도 주요 특성은 유지된다는 것을 의미
ITE-AE에서 noise haed의 영향력에 대한 ablation study 시행
head가 이상적인 noise를 손실 계산식(아래)의 균형으로 예측
$\mathcal{L} = \alpha \cdot \mathcal{L}_{\text{MSE}}(X, Y_{\sigma}) + (1 - \alpha) \cdot \mathcal{L}_{\text{MSE}}(s_{\sigma}, s_t)$
방법: $\alpha=0.5$로 두고, 타겟 표준편차 $s_{t}$ 를 그림과 같이 다양하게 바꾸어가며 실험

실질적으로 이상적인 표준편차를 𝛴의 표준편차로 만드는 것이 좋은 합성데이터 샘플을 만들 수 있게 함
-> 주 도메인의 표준편차 공유가 𝛴' 생성을 활성화하기 때문
$\nexists N_{head} $ for $s_{t}=0\rightarrow$ 함수 관게에 의해 output은 biased
$s_{t} \uparrow$ -> noisy 추정 심해짐(주성분 신호는 여전히 학습되고 인식되지만)
head 파라미터화는 ITF-FM의 noise 수준을 통제가능하게함 <-> ITF-GAN은 선행지식 𝛴없이 자동으로 noise 파라미터 추정
[특이 사항]:
함수, 파라미터, 조합론(combinatorics)를 이용하여 해석가능하게 만듦
ITF-FM: series를 해석가능한 notation으로 변형하여 feature(계절, 영향력 등) 조정 가능하게 함
feature 조작중인 합성데이터의 latent space
The latent represemtation shift for 조정 시각화

보통의 선형, 합성곱 특성들은 고차원 decoder 구조이므로 직관적 해석, 통제 불가
합성 파라미터 분포는 도메인 소스 분포와 일치하고, 이것으로 유사한 샘플 생성 -> 분포 샘플로 모델링 잘 함
ITF-GAN: 생성된 시계열의 해석가능성과 sequential encoding이 큰 이점이지만, MS 데이터의 Wave-GAN의 경우, 같은 패턴의 출력이 종종 생성되는 문제점이 있음. 이 문제점은 Wasserterin loss를 통한 손실 계산 최적화를 통해 극복할 수 있음.
[5] 결론
이 방법은 구별불가능한 합성데이터를 분야 상관없이 생성 가능했고, 심지어 feature space에서 완전히 해석이 가능함
'TechStudy > SyntheticData' 카테고리의 다른 글
| TF리뷰 (0) | 2024.07.03 |
|---|---|
| Nemotron: LLM훈련을 위한 합성데이터 생성모델 (0) | 2024.06.20 |
| 합성데이터 사례: 서울시민 라이프스타일 (0) | 2024.06.19 |
| 합성데이터 사례: 기업개요 및 주주 신용등급 (0) | 2024.06.18 |
| 합성데이터 사례: 통신사 멤버십 사용내역 (0) | 2024.06.18 |


