인공지능(AI) 기초

출처: AI 엔지니어 기초 다지기 : 네이버 부스트캠프 AI Tech 준비과정

 

 

 

AI모형 설계에 중요한 세 가지: 구현 능력(Implementation skills), 수학적 사고능력(Linear Algera, Probability), 최근 논문 트랜드 파악

 

 

Key Components of Deep Learning: (대표적 4가지; 논문 리딩에서 주의깊게 봐야할 부분)

1) The data that the model can learn from

Data 예시: 문제 해결 대상에 따라 양상이 달라진다.

Classification: 사진을 분류하는 문제

Semantic Segmentation: 픽셀 단위로 dense classification하는 것

Detection: 영역(bounding box)를 찾아내기

Pose Estimation: 사람들의 3차원 스켈레톤 정보 추출하기

Visual Q&A: 질문하는 것에 대해 이미지를 바탕으로 답하는 문제

 

 

 

 

 

 

 

 

2) The model of how to transform the data

모델의 예제

데이터를 받아서 특정 결과, 의도, 목적에 맞게 결과물을 가져오는 tools

 

 

 

 

 

 

 

 

 

 

3) The loss function that quantifies the badness of the model: a proxy(근사치) of what we want to achieve,

왜 근사치?: 항상 값을 작게 만든다고해서 원하는 목적을 달성한다는 보장이 없기 때문

데이터와 모델이 정해져있을 때, 모델을 어떻게 학습할 지에 대한 기준

 

목적에 따라 달라지는 loss funtions(Mean Square Error, Cross Entrophy, Maximum Likelihood Estimation)

이 대표적인 예가 항상 일치하지 않음에 유의한다.

-> Loss function이 어떤 성질을 갖고 있고 이것이 왜 내가 원하는 결과를 얻어낼 수 있는지를 알아야 함!

 

 

 

 

 

 

 

 

 

 

 

4) The algorithm to adjust the parameters to minimize the loss (최적화방법)

학습을 규제(Regulaization)하는 것을 포함한다.

 

 

 

 

 

 

 

 

이 4가지를 중점적으로 봐야 기존에 비해 어떤 장점 혹은 contribution이 있는지 이해하기 쉽다.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

Historical Review

그동안 딥러닝 발전 양상이 어떠했는지 해당 논문을 기반으로 중요한 포인트를 파악해보자.

 

AlexNet (2012)

딥러닝이 실질적으로 성능을 발휘하고 기계학습 판도가 바뀌게 된 계기이다.

 

 

 

 

 

 

 

 

DQN (2013)

알파고를 만든 deepmind(현재는 구글에 인수되어 google deepmind) 회사에서 게임을 강화학습으로 풀어낸 것.

오늘날의 deepmind를 있게 한 논문이다.

 

 

 

 

 

 

 

 

 

Encoder / Decoder (2014)

외국어 단어를 벡터에 넣어 인코딩을 하고 그것을 영어 단어의 sequence를 만들어 디코딩하는 것. (외국단어 해독하기)

Natural Machine Translation(기계화 번역) 트랜드 발달 계기

 

 

 

 

 

 

 

 

Adam Optimizer (2014)

학습할 떄 최적화를 잘 해주는 Adam. 성능이 좋다. 왠만하면 잘된다 라는 것을 보장해준 최적화 방법.

보통 논문에 파라미터 조정이나 왜 이 방법을 써서 최적화했는지 설명이 없다면, 이는 그렇게 안하면 결과가 안나오기 때문

 

 

 

 

 

 

 

 

 

 

GAN; Generative Adversarial Network (2015)

Les Trois Bresseurs라는 술집에서 술이 맛없어서 생각하다가 떠올랐다고 함.  (술마시다가 연구에 도움된 사례)

Network가 Generator와 Discriminator 2개를 만들어서 학습을 시키는 것이다.

이미지(혹은 텍스트)를 어떻게 generate하는지에 대한 것이다.

중요함!

 

 

 

 

 

 

 

 

 

ResNet; Residual Networks (2015)

딥러닝을 딥러닝답게(Neural Network를 깊게 쌓는 것) 만든 논문. 

ResNet 이전에는 네트워크를 많이 쌓으면 학습은 좋지만 test가 안좋았음.

ResNet은 네트워크를 기존보다 더 깊게 쌓아도 test 결과가 좋도록 만들어줌(물론, 지나치면 test 안좋아짐)

 

 

 

 

 

 

 

 

 

 

 

 

Transformer from Attention Is All You Need (2017)

중요함!

 

 

 

 

 

 

 

BERT; fine-tuned NLP models (2018)

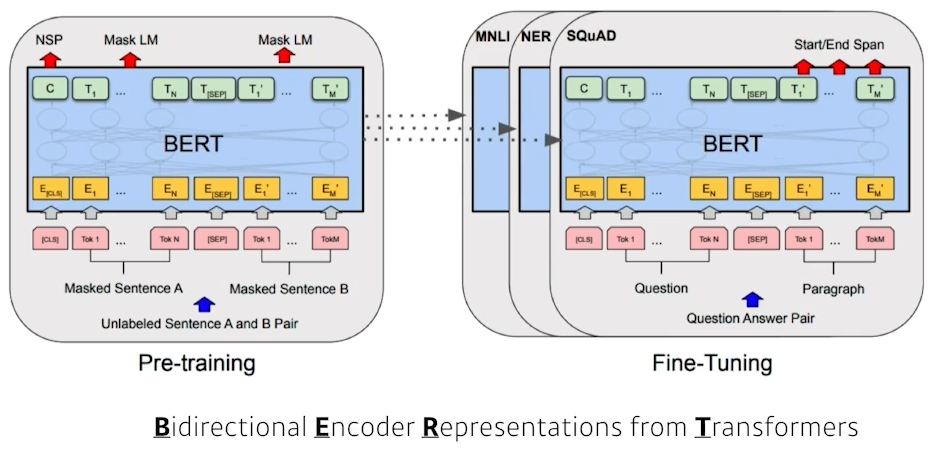
BERT는 앞의 Transformer에 Bidirectional Encoder를 사용하는 것이다.

fine-tuned NLP(자연어처리) model은 인터넷의 많은 말뭉치를 free training함.  (이게 point)

 

 

 

 

 

 

 

 

 

 

 

 

 

Big Language Models; GPT-X (2019)

Fine-tuned NLP model의 끝판왕. 175억개의 파라미터 사용 (아무나 학습 못시킴)

 

 

 

 

 

 

 

 

 

 

 

Self-Supervised Learning (2020)

학습데이터는 한정적인데 여기선 주어진 학습 데이터 외 label을 모르는 unspupervised data를 사용함.

(구글 데이터 비지도 학습)

 

이 이후 Self-Supervised Learning 이라는 단어가 포함된 논문들이 많아짐

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

---

 

딥러닝 공부할 때 권장되는 포인트

 

정의1)

Neural Networks: computing systems vaguely inspired by the biological neural networks that constitute animal brains

시작은 뉴런의 모방이지만 이걸 굳이 사람의 뇌를 모방했다는거에 집중하기보다는 왜 잘 되었는지, 수학적으로 분석하는게 옳지 않을까?

 

정의2)

Neural Networks: function approximators that stack affine transformations followed by nonlinear transformations

이런 수학적인 정의가 좀 더 직관적이고 이해하기 쉽지 않을까?

Neural Networks 예제

 

 

 

 

 

 

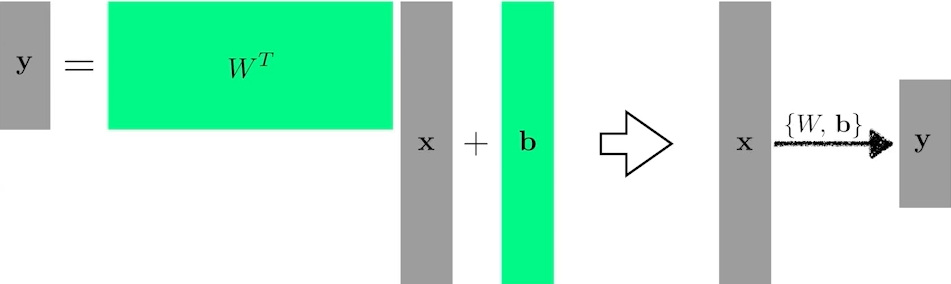
간단하게 선형형태에 대해 알아보자.

Linear Neural Networks 예제

loss function을 줄이는 것이 목표 -> 어떤 파라미터를 움직여야 줄어들까?

이 과정을 통해 w와 b 값을 갱신한다.

 

이 과정이 계속 진행되는 것이 Gradient Descent이다.

cf) loss function <->

     reward function(이 경우 Gradient Ascent)

 

Stepsize 매우 크면 학습X (G.D가 local한 정보이므로)

-> 적절한 Stepsize 설정 필요

-> Adaptive Learning으로 Stepsize 자동 설정함

 

 

 

여기서 차원을 늘리려면 Affine Transformation 개념이 적용된다.

W: weight, b: bias

해석방법: 두 개의 벡터 스페이스(서로 다른 두 차원) 사이에 선형변환 ; a mapping between two vector spaces

 

 

 

결국 딥러닝은 neural network를 여러 개 쌓겠다는 것. 그러면 어떻게 쌓을까?

 

 

단순히 선형 결합을 여러 번 반복하는 것은 여러 개 쌓는 것이 아님을 유의한다!

잘못된 예: 이건 한 단 짜리 network와 동일하다.

 

 

 

 

 

선형결합할 때마다 activation function(ReLu, sigmoid 등)을 곱하여서 표현력을 다양하게 유도한다. 

이렇게 쌓아야 네트워크 쌓는 것이 유의미해진다!

어떤 것이 좋은지는 정해져있지 않다. 그때그때 다름

 

 

 

 

Universial Approximaton Theorem: Neural Nework가 좋은 근거

이 Theorem은 이런 좋은 network가 존재한다는 것을 증명할 뿐, 내가 만드는 network가 항상 이런 성질을 가진다는 것을 보장하지 않는다!

히든레이어 하나 있는 뉴럴 네트워크는(또는 뉴럴 네트워크의 표현력은) 대부분의 continous function을 포함(근사)한다.

 

 

 

 

 

Multi-Layer Perceptron(MLP): the class of architectures. 최소 한 개 hidden layer가 있는 두 layer network

신경망이 여러개 합성된 함수.

입력이 주어져있고, affine transformation에서 히든 벡터가 나오고 그 벡터의 히든 레이어에서 다시 연결.

h = hidden layer(hidden vector)  // h는 여러개가 될 수 있다.

 

 

 

Loss function 각각의 원리를 잘 알아두자.

 

 

 

 

 

 

 

Generalization: How well the learned model will behave on unsee data (일반화 성능)

보통 일반화 성능 높이는게 목표이다.  -> Training error, Test error의 차이를 의미함

성능이 좋다 = 해당 네트워크 성능이 학습 데이터와 비슷하게 나올 것임을 의미 (단 train성능 자체가 안좋으면 의미 없음)

Underfitting:네트워크가 너무 간단하거나 학습이 적은 경우&nbsp; // Overfitting: train결과는 좋은데 test에서 망함

 

 

 

(K-fold) Cross-validation: a model validation technique for assessing how the model will generalize to an independent (test) data set

학습 데이터를 k-1개로 나눠서 각각 학습시키고 나머지 1개로 test를 하는 것(validation) 

 

학습에서는 train과 validation data만 써야 하고, test data는 사용해선 안된다.

이 과정을 통해 하이퍼 파라미터 값을 찾는다.

 

 

 

 

 

Bias: input에 대해서 평균적으로 target에 접근한 정도. 예측값과 얼마나 멀이 떨어져있는 지에 대한 것.

Variance: input에 대해서 출력이 얼마나 일관적으로 나오는지 (낮으면 일관적, 크면 많이 달라짐), 예측값들의 차이.

 

Bias and Variance Tradeoff Theorem: Bias와 Variance는 Trade-off 관계이다.

노이즈(noise)가 있는 학습데이터에 대해서 ∃noise인 target을 최소화할 때, 해당 target은 bias, variance, noise 3가지로 나눌 수 있다. (bias 줄이면 variance가 올라감)  -> bias와 variance를 둘 다 줄여야함 (그러나 둘 다 줄이기 어려움)

 

 

 

 

 

 

 

 

 

 

 

 

bootstraps: 신발끈

Bootstrapping: any test or metric that uses random sampling with replacement

data를 여러번 random subsampling

 

 

Bagging(Bootstrapping aggreaging): bootstrapping해서 모델 여러 개 만들고 각각 독립적으로 결과 ensemble(종합)하는 것

ex) ensemble

 

 

Boosting: combining weak learners(약한 모형), specific training samples that are hard to classify, in sequence to build a strong model. (각 learner들은 이전 weak learner의 실수로부터 배움이 있음)

 

여러개 모델 만드는 것은 같지만 boosting은 결과적으로 weak learners들을 sequnentially 개선해서 하나의 강한 모형 만듦 

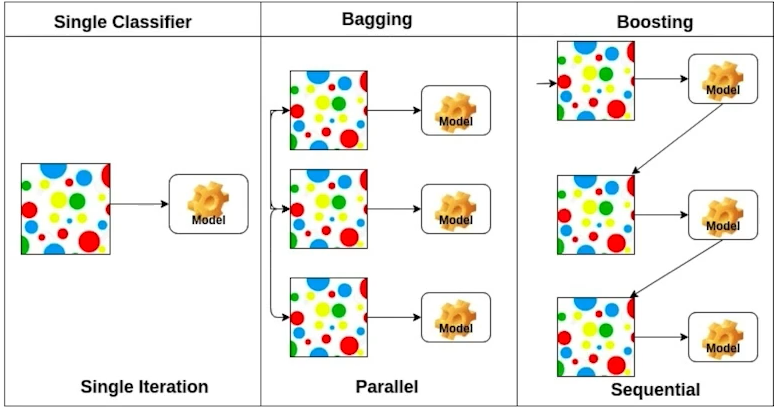
Single Classifier: data에 대해 하나의 모델 만드는 것

 

 

 

 

 

 

 

 

---

Practical Gradient Descent Methods

Gradient Descent: First-order iterative optimization algorithm for finding a local minimum of a differentiable function

local minimum을 찾는 FOC (편미분) 알고리즘으로 대표적 방법이 3가지가 있다.

Stochastic Gradient descent(SGD): update with the computed gradient from a single sample (가장 기본 형태)

W를 계속해서 업데이트하는 양상이다. // Learning rate(에타) = step size

문제점: Learning rate(step size) 적절히 설정하는 것이 어려움

 

 

Mini-batch Gradient descent(MGD): update with the computed gradient from a subset of data 대부분의 딥러닝에서 씀

Batch Gradient descent(BGD): update with the computed gradient from the whole data

 

 

 

Batch-size matters: batch-size 문제는 매우 중요하다! (아래 논문을 보자)

On Large-batch Training for Deep Learning: Generalization Gap and Sharp Minima, 2017

Large batch쓰면 일반화 능력 감소로 모델 성능 저하됨. 즉, batch-size 작게 쓰는게 일반적으로 성능이 좋다. (flat min 선호)

Large batch -> tend to converge to sharp minimizer

Small batch -> consistently converge to flat minimizer

이유: inherent noise in the gradient estimation

 

Flat-min은 train과 test의 local minimum 차이가 적음 // sharp-min은 조금만 달라져도 train과 test 괴리가 심해짐

small batch size로 나온 flat-min은 generalizing performance가 좋은 경향 있음

 

 

 

 

 

 

 

Momentum(관성): 적절한 Learning rate 설정 문제를 최적화하기 위해 나온 기본 최적화 테크닉

accumlated gradient로 update하는 방법이다.

beta(momentum): 하이퍼 파라미터

장점: gradient의 방향을 일관적으로 잘 유지시켜줌.

단점: 해당 경향성(momentum)으로 인해서 내려갔다 올라갔다가 계속 반복되어 local minimum에 도달을 못하거나 시간이 오래걸릴 수 있음

 

 

 

 

 

 

 

 

 

Nesterov Accelerated Gradient(NAG): 움직이는 방향의 경향을 기록(momentum)하는 것이 아닌, 움직여서 도착한 새 점에서 gradient를 계산함

장점: momentum보다 좀 더 빠르게 local minimum에 converge(이론적으로 converging ratio 더 빠름)

 

 

 

 

 

 

 

 

 

 

Adagrad: 적게 변하는 파라미터는 많이, 많이 변하는 파라미터는 적게 변화시키는 adaptive learning rate 사용.

문제점: G는 계속해서 커짐 -> 무한할 경우(the training for a long period), W 업데이트 안됨 -> 학습이 멈춰짐

 

 

 

 

 

 

 

 

 

 

Adadelta: Adagrad의 G가 계속 커지는 문제점을 막기위한 방법.

 

Timestep t에 대해서 시간의 변화 Gt를 본다. (문제점: 이전의 모든 정보가 있어야함)

-> 첫 번째 Gt식은 이 문제점을 보완하는  expoential moving average(EMA) 방법이다.

문제점: learning rate가 없음 -> 바꿀 수 있는 요소가 별로 없음 -> 많이 활용되지 않음.

 

 

 

 

 

 

 

RMSprop: an unpublished, adaptive learning rate method by Geoff Hinton in his lecture

Geoff Hinton이 딥러닝 강의하다가 '이렇게 하니까 잘되더라' 하던 것이 유명해짐. 논문으로 따로 보고된 기법이 아님따라서 논문에서 인용시 보통 Geoff Hinton의 lecture를 출처로 두곤 했음.

idea(원리): Gt는 EMA를 하고, Adagrad의 W 갱신 방법에서 stepsize를 분자에 추가한 것이 전부이다.

 

 

 

 

 

 

 

 

Adative Moment Estimation(Adam): Momentum + EMA of Gt

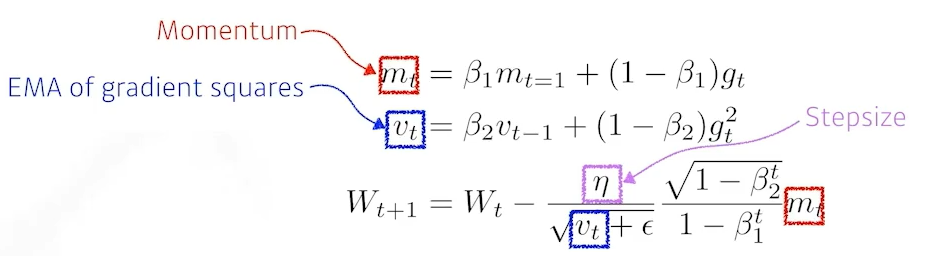
원리: 뒤 1-beta 분수는 unbiased estimator가 되기위한 수학적인 장치(증명됨)

가장 잘되는, 무난하게 잘되는 방법이다.

ε : divided by zero를 막기위한 파라미터. 이 파라미터를 조정하는게 실질적으로 중요함!

---

Regularization(규제)

Generalization을 잘 할 수 있도록 학습을 규제한다.

 

 

Early stopping: loss가 커지는 경향이 보이면 훈련 중단

조건: additional validation data가 필요함

 

 

 

 

 

 

 

Parameter norm penalty(=Weight decay): Adding smoothness to the function space

Neural network parameter가 너무 커지지 않도록 하는 것

 

.

 

 

 

 

 

Data augmentation: 데이터가 많으면 잘됨. (현실적으로는 데이터 한계가 많으므로 적절하게 확장한다.)

적은 데이터는 ML, 많은 데이터는 AI에 적합하다

image data augmentation의 예제들 (각도변환)

 

 

 

 

 

 

 

 

Noise robustness: Adding randnom noises inputs or wrights

 

 

 

 

 

 

 

 

 

 

 

 

 

Label smoothing: 학습데이터 2개를 뽑아서 섞어서(mix-up) augment training examples

이미지 분류의 decision boundary를 찾아서 이 boundary를 부드럽게 만들어주는 효과가 있다.

Cutout(특정 이미지 빼버림) //&nbsp; CutMix 예제(특정 영억 섞기)

실질적으로 Mixup이나 CutMix를 쓰면 한정된 이미지 데이터 분류문제에 효율적으로 모델 성능을 올릴 수 있는 경우가 많다.

 

 

 

 

 

 

 

 

 

 

 

 

Dropout: randomly set some neurons to zero.

해석: 이를 통해 각 neuron들이 좀 더 robust features를 잡는다. (엄밀한 수학적 증명이 되진 않음)

 

 

 

 

 

 

 

 

 

 

 

 

 

Batch normalization: 적용하고자하는 (dimension)layer's statistics(mean, variance)를 정규화(normalization)하는 것 -> Internal Covariate(feature) shift를 줄일 수 있음 -> network 학습 잘 됨

Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, 2015

Internal Covariate Shift을 줄일 수 있다는 것에 대한 논란이 많은 논문 (많은 논문이 동의하지 않음)

But, 이 방법을 사용하면 깊은 layer에 대해서 성능이 올라가는 것은 분명함

간단한 분류문제에서 성능올리는 데에 도움 

 

 

Batch Norm 외의 다양한 Normalization 방법들

Batch Norm: Layer 전체

Layer Norm: 각 Layer에 대해서

Instance Norm: 각 데이터 한 장에 대해서

Group Norm: Layer와 Instance Norm의 중간 형태  (Group Normalization 2018)

 

 

 

 

 

 

 

 

---

기존 선형모델 구조 복습

O=WX+b&nbsp; // W = 가중치 행렬, b= 절편

선형모델 수식 해석방법

 

인공지능모형은 비선형모델이다.

 

 

화살표 = w(가중치) -> 딥러닝 개념 연관

 

 

 

 

softmax함수를 구현하고 출력하기

np.max를 빼는 이유: 지수함수 np.exp가 매우 큰 값이라 overflow 가능성을 방지하기 위함

 

결론: train(학습)때 softmax 사용. 출력 때는 사용 X

 

 

 

 

 

H = hidden vector, 뉴런

 

 

 

 

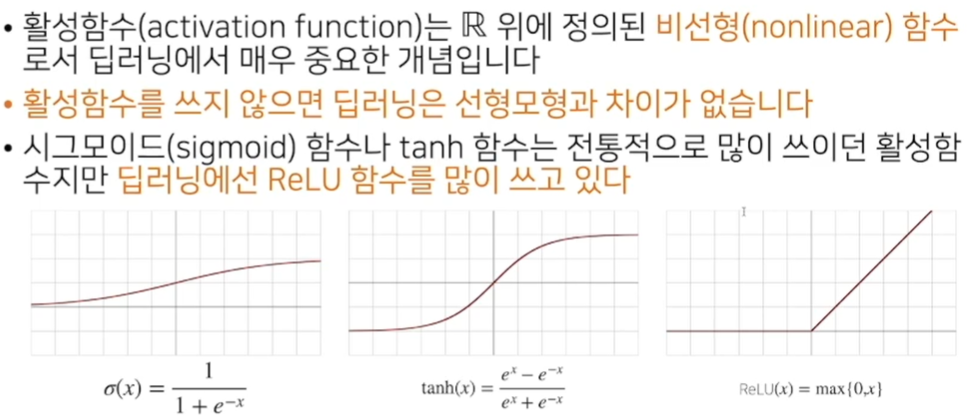
맨 오른쪽 ReLU가 요즘 쓰는 함수이다.

 

 

왜 층을 여러개 쌓을까? : 층이 깊음 -> 목적함수 근사에 필요한 뉴런(노드) 숫자 빨리 줄음 -> 효율 학습 可

cf) Universal Approximation Theorem: 이론적으로 2층 신경망으로도 임의 연속 함수 근사 可

 

 

 

 

 

 

역전파 알고리즘: 각 층의 손실함수에 대한 미분을 계산할 때 사용. 윗층 계산해서 밑층 계산하는 것

빨간 화살표: 윗층의 gradient정보를 바탕으로 해당 밑층(저층)을 계산

 

 

Backpropagation은 연쇄법칙(chain-rule; 합성함수 미분법) 기반 자동미분법을 사용한다

컴퓨터가 기억 = 메모리 사용

자동미분법을 사용하기위해 컴퓨터 메모리를 상대적으로 많이 사용한다.

Forwardpropagation은 자동미분 사용을 안하므로 메모리도 사용하지 않음(차이점!!)

 

 

Ex) Two-layers network(2층 신경망)

 

 

이렇게 계산한 각각의 가중치행렬에 대한 grdient vector를 SGD확률적 경사하강법, 미니batch를 통해 데이터를 번갈아가며 학습해서 주어진 목적식을 최소화하는 파라미터 발견 -> 이 원리가 딥러닝 학습 원리

 

결론: 딥러닝은 선형모델 + 활성함수들로 이뤄진  합성함수 -> chain rule 필요 -> chain rule을 적용한 학습 알고리즘으로 backpropagation을 사용