인공지능 기본 수학 (확률론, 통계)

출처: AI 엔지니어 기초 다지기 : 네이버 부스트캠프 AI Tech 준비과정

 

 

 

 

확률론 왜 필요? :  딥러닝(AI)는 확률론 기반 기계학습 이론을 근거로 하기 때문

분산 및 불확실성 최소화위해서 측정 방법(통계학에서 제공, 확률론 기본 개념)을 알아야 함

 

기계학습내 손실함수(loss function): 데이터 공간 통계적 해석 유도

ex) 회귀분석내 손실함수 L2노름: 예측오차 분산 최소화 방향으로 학습 유도

ex) 분류문제내 cross-entropy(교차엔트로피)는 모델 예측 불확실성 최소화 방향 학습 유도

 

 

데이터 공간 x y 에서 D는 데이터 분포

Y: 정답 레이블  // 파란색 점 = 관측한 데이터

 

discrete(이산형) <-> continuous(연속형) 확률 변수 구분 기준: 확률분포 D

확률질량함수

 

확률밀도함수(기계학습에서 많이 사용함)

 

cf) 이산형과 연속형이 둘 다 있는 경우도 있다. 반드시 이분법으로 나눌 수 없다!

 

 

Joint Distribution(결합분포) P(x,y)는 기존 확률분포 D를 모델링한다.

p(X) = 입력 x에 대한 Marginal distribution (주변확률분포; y정보 없음)

P(x|y) = input x, output y 관계 모델링

 

X값의 빈도를 나타냄(Marginal distribution)                                     //    조건부 확률 분포 P(xy): 특정 조건의 데이터 확률 분포. 그림은 Y=1인 경우이다.

 

P(x) = 각 결합분포의 y의 합 = 각 결합분포를 y로 적분

y가아닌 x에 대해서 하면 y에 대한 주변확률 분포를 구할 수 있다.

 

 

조건부확률은 기계학습에서 중요하다!

P(y|x) : input x에 정답이 y일 확률(연속분포는 확률이 아닌 밀도로 해석)  <-> P(x|y) = input x, output y 관계

조건부기댓값 사용 이유: L2노름을 최소화하는 함수와 일치하기 때문

조건부 기댓값을 사용안하는 경우 ex) 데이터를 robust하게 예측하는 경우 median(중앙값)을 사용해서 추정하기도 한다.

 

 

 

 

 

Expectation 정의

기댓값(expectation): 데이터를 대표하는 통계량

 

 

 

 

 

 

기계학습의 현실: 확률분포 명시적으로 알 수 없음 -> 이 상황에서 기댓값을 계산하려면? -> Monte Carlo 샘플링 사용

 

Monte Carlo sampling condition: if it is independent trials, by Law of large number(대수의 법칙), it converges.

몬테카를로 각종 예제

이 적분값은 해석적으로 구하는 것은 불가능하다 -> 균등분포 데이터를 집어넣고 근사시킴.

 

Monte Carlo없이 수치적으로 근사를 시킨 경우(왼쪽 위) <-> Monte Carlo를 사용한 근사 구현(오른쪽)

Monte Carlo로 근사시키려면? : Uniform distribution(균등 분포)에서 data sampling -> 함수 대입 -> 대입된 값을 산술평균 취해줌 -> 구간의 길이(2)를 곱함

 

 

 

 

---

 

 

통계적 모델링: 적절한 가정에 확률분포 추정(inference) = 기계학습, 통계학의 공통 목표

다양한 확률분포의 종류

 

모집단 분포 정확히 알아내는 것은 불가능 -> 근사적으로 확률분포 추정 (데이터, 추정방법 불확실성 위험 최소화)

모수(parameter): 확률분포를 결정하는 지표. ex) 평균, 분산 등

모수적(parametric) 방법론: 데이터가 특정 확률분포를 따른다고 선험적(a priori) 가정한 후, 그 분포를 결정하는 모수(parameter)추정하는 방법

비모수(nonparametric) 방법론: 특정 확률분포 가정 없이 모델 구조 및 모수 개수가 유연하게 바뀌는 경우. 모수가 무한히 많거나 데이터에 따라 바뀌는 경우에 해당. (모수가 없다는 의미가 아님!) 대부분의 기계학습의 방법론에 해당

 

모수, 비모수 방법론 차이: 특정 확률분포 가정 여부

 

 

주의점: 기계적(공식적)으로 확률분포 가정하면 안됨! 항상 데이터 생성 원리를 먼저 고려하는 것이 원칙!

각 분포마다 검정방법이 있으므로 모수 추정 후에는 반드시 검정해야함!

 

데이터 확률분포 가정 후 모수를 추정하는 예제: 정규분포로 가정한 경우

불편추정량 -> 기댓값 E를 적용할 때 모집단 모수와 일치하도록 유도하기 위함

 

 

Sample distribution(표본분포): 표본들의 분포

Sampling distrbution(표집분포): 통계량(표본평균, 표본분산 )의 확률분포

두 분포 개념 정의가 다름에 유의! 

표본평균의 표집분포에 대한 설명이다.

모집단 분포가 정규분포가 아님 -> 표본분포도 정규분포 아님

BUT 통계량의 확률분포(표집분포)는 정규분포를 따를 수 있다.

데이터 개수 N이 증가하면서 통계의 베르누이(이항)분포의 모양이 정규분포(분산이 0으로 가까워짐)를 따르는 모습이다.

 

 

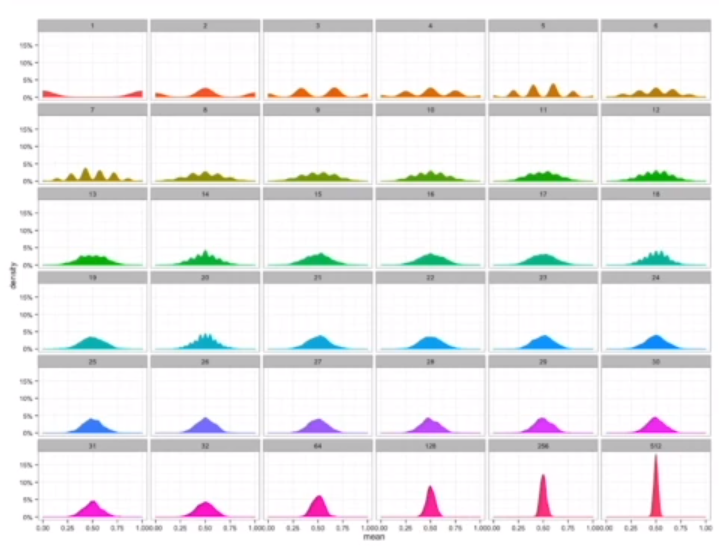
그렇다면 적절히 사용해야할 통계량을 선정하는 기준은 무엇일까?

표본평균, 표본분산: 중요한 대표 통계량 but 확률분포마다 사용하는 모수 다름 -> 적절한 통계량 달라질 수 있음

 

MLE(Maximum Likelihood Estimation: 최대가능도 추정법): 이론적으로 가장 가능성 높은 parameter(모수) 추정

확률이 아니라 대소비교가 가능한 함수로 해석해야한다.

로그가능도 사용 이유: 데이터 숫자가 수억단위인 경우, 컴퓨터 계산 불가능,

경사하강법(=미분을 사용)으로 가능도 최적화할 때, 로그가능도 연산량 O(n^2) -> O(n) 로 줄어든다.

손실함수에 사용된 경사하강법 -> 음의 로그가능도(negative log-likelihood) 최적화(최소화)

 

 

 

 

 

 

 

MLE 정규분포 예제

최적화하는 세타를 찾는 문제이다.

정규분포: 2개의 모수(평균, 분산)을 사용함 -> 이와같이 식을 변형할 수 있다.

 

log로 계산해보면

log likelihood를 평균 mu로 편미분한 경우와 표준편차 sigma로 편미분한 두 식이 0이되는 mu와 sigma를 찾아보자

분산MLE의 mu값은 위 MLE에서 도출된 mu값을 대입할 수 있다. // 분산MLE 분모가 n-1이 아니므로 불편추정량 보장하지 않는다.

 

 

 

 

 

 

 

 

 

 

 

MLE 카테고리분포 예제

P1 .. Pd : 카테고리분포 모수&nbsp; &nbsp;//&nbsp; &nbsp;d: 차원 개수

여기서 로그연산은 다음과 같이 진행된다

 

 

 

 

 

nk: k=1인 xi개수

 

 

라그랑지 최적화(승수법) 적

 

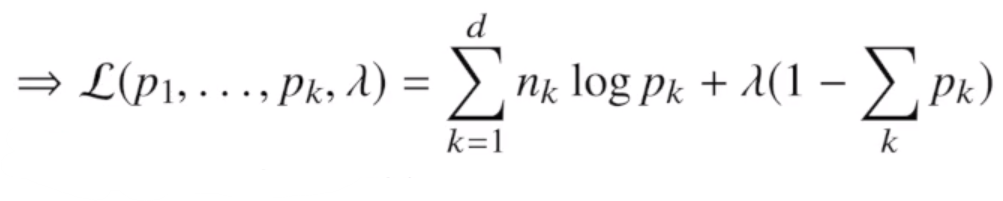
라그랑지 최적화, FOC(미분) 결과는 다음과 같다.

결국 Pk 값은&nbsp; nk / n&nbsp; 로 표현됨 -> Pk값(모수)은 각 해당 차원의 데이터 숫자의 비율이다.

 

 

 

 

 

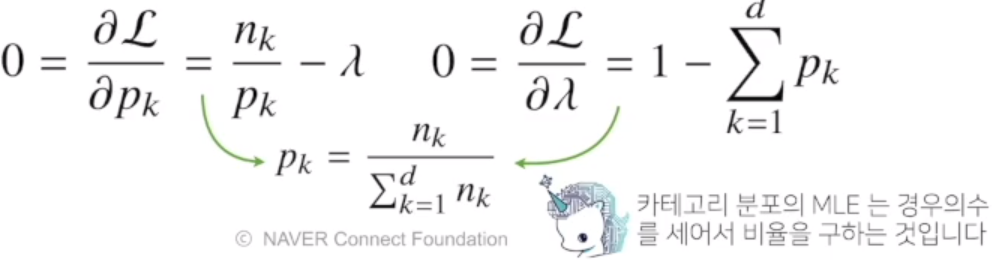
MLE로 딥러닝에 기계학습모델 학습하기 (해당 수식 유념할 것)

K: 모든 클래스 개수 // n: 데이터 개수 // y: 정답 레이블

 

기계학습에 사용되는 손실함수: 모델이 학습하는 확률분포, 데이터에서 관촬된 된 확률분포 이 둘의 거리로 유도

 

 

 

 

[point]

각종 논문들을 보면 이 MLE 원리에 따라서 손실함수 최적화가 유도됨

통계학적 방법을 통해 기계학습이 이뤄짐