scipy랑 쓰면 공학 소프트웨어 MATLAB 기능 수준
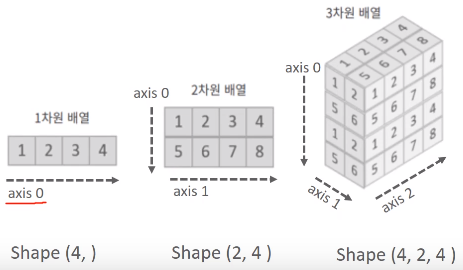
각 차원(dimension) = axis로 표현
ndarray의 axis축
- 행, 열, 높이가 아니라 axis0, axis1, axis2같이 axis단위로 부여
ndarray 생성, 초기화 방법
- ndarray를 편리하게 생성하기 - arange(array + range)
- python의 range처럼 순차적으로 증가하는 값으로 ndarray 생성
array = np.arange(10)
print(array)
print(array.dtype, array.shape)[0 1 2 3 4 5 6 7 8 9]
int32 (10,)
Numpy.ndarray의 다양한 속성값
ndarray.shape : 배열의 각 축(axis)의 크기
ndarray.ndim : 축의 개수(Dimension)
ndarray.dtype : 각 요소(Element)의 타입
ndarray.itemsize : 각 요소(Element)의 타입의 bytes 크기
ndarray.size : 전체 요소(Element)의 개수
a = np.arange(15).reshape(3, 5)
print(a)
print(a.shape) # (3, 5)
print(a.ndim) # 2
print(a.dtype) # int64
print(a.itemsize) # 8
print(a.size) # 15
print(type(a)) # <class'numpy.ndarray'>
ndarray를 편리하게 생성하기 - zeros
- 선언한 크기만큼 0으로 채워진 ndarray 생성
zero_array = np.zeros((3,2),dtype='int32')
print(zero_array)
print(zero_array.dtype, zero_array.shape)[[0 0]
[0 0]
[0 0]]
int32 (3, 2)
ndarray를 편리하게 생성하기 - ones
- 선언한 크기만큼 1로 채워진 ndarray 생성
- dtype을 설정하지 않으면 기본으로 실수형으로 선언됨
one_array = np.ones((3,2))
print(one_array)
print(one_array.dtype, one_array.shape)[[1. 1.]
[1. 1.]
[1. 1.]]
float64 (3, 2)
np.arange() 와 np.linspace()를 이용하여 연속적인 데이터도 쉽게 생성
- np.arange(): N 만큼 차이나는 숫자 생성
- np.linspace(): N 등분한 숫자 생성
print(np.arange(0, 2, 0.3)) # 0이상 2미만 까지 0.3씩 차이나게 생성[0. 0.3 0.6 0.9 1.2 1.5 1.8]
x = np.linspace(0, 99, 100) # 0~99까지 100등분
print(x)[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17.
18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35.
36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53.
54. 55. 56. 57. 58. 59. 60. 61. 62. 63. 64. 65. 66. 67. 68. 69. 70. 71.
72. 73. 74. 75. 76. 77. 78. 79. 80. 81. 82. 83. 84. 85. 86. 87. 88. 89.
90. 91. 92. 93. 94. 95. 96. 97. 98. 99.]

차원과 크기를 변경
- reshape() 로 ndarray를 특정 차원 및 형태로 변환
- 변환 형태를 reshape()의 인자로 전달
- -1을 전달하면 특정 차원으로 고정된 가변적인 ndarray형태 변환
- -1 값은 1개의 인자만 입력해야 함

array1 = np.arange(10)
print('array1:\n', array1)
array2 = array1.reshape(2,5)
print('array2:\n',array2)
array3 = array1.reshape(5,2)
print('array3:\n',array3)array1:
[0 1 2 3 4 5 6 7 8 9]
array2:
[[0 1 2 3 4]
[5 6 7 8 9]]
array3:
[[0 1]
[2 3]
[4 5]
[6 7]
[8 9]]
값이 원소 개수와 안맞는 reshape 입력시 value error
-1 예제
- col axis 크기 5에 고정, row axis크기 이에 맞춰 자동 변환. 즉 2x5 형태 변환
array2 = array1.reshape(-1,5)
print('array2 shape:',array2.shape)array2 shape: (2, 5)
- row axis 크기 5 고정, col axis크기는 이에 맞춰 자동 변환. 즉 5x2 형태 변환
array3 = array1.reshape(5,-1)
print('array3 shape:',array3.shape)array3 shape: (5, 2)
역시 이 경우도 숫자 (-1,4) 처럼 원소 개수가 안맞으면 error.
array1 = np.arange(8)
print('array1:\n',array1)
array3d = array1.reshape((2,2,2)) #3차원 형성
print('array3d:\n',array3d.tolist())
print('array3d shape:',array3d.shape)
array5 = array3d.reshape(-1,1) # 3차원 ndarray를 2차원 ndarray로 변환
print('array5:\n',array5.tolist())
print('array5 shape:',array5.shape)
array6 = array1.reshape(-1,1) # 1차원 ndarray를 2차원 ndarray로 변환
print('array6:\n',array6.tolist())
print('array6 shape:',array6.shape)
array7 = array1.reshape(1,-1) # 1차원을 2차원으로 변환, 단 row가 길어짐
print('array7:\n',array7.tolist())
print('array7 shape:',array7.shape)array1:
[0 1 2 3 4 5 6 7]
array3d:
[[[0, 1], [2, 3]], [[4, 5], [6, 7]]]
array3d shape: (2, 2, 2)
array5:
[[0], [1], [2], [3], [4], [5], [6], [7]]
array5 shape: (8, 1)
array6:
[[0], [1], [2], [3], [4], [5], [6], [7]]
array6 shape: (8, 1)
array7:
[[0, 1, 2, 3, 4, 5, 6, 7]]
array7 shape: (1, 8)

Matrix는 list와 달리 comma(,) 가 없다.
array1d = np.arange(start=1, stop=10)
array2d = array1d.reshape(3,3)
print(array2d)
print('(row=0,col=0) index 가리키는 값:', array2d[0,0] )
print('(row=0,col=1) index 가리키는 값:', array2d[0,1] )
print('(row=1,col=0) index 가리키는 값:', array2d[1,0] )
print('(row=2,col=2) index 가리키는 값:', array2d[2,2] )[[1 2 3]
[4 5 6]
[7 8 9]]
(row=0,col=0) index 가리키는 값: 1
(row=0,col=1) index 가리키는 값: 2
(row=1,col=0) index 가리키는 값: 4
(row=2,col=2) index 가리키는 값: 9
mtx indedxing
array1d = np.arange(start=1, stop=10)
array2d = array1d.reshape(3,3)
print('array2d:\n',array2d)
print('array2d[0:2, 0:2] \n', array2d[0:2, 0:2])
print('array2d[1:3, 0:3] \n', array2d[1:3, 0:3])
print('array2d[1:3, :] \n', array2d[1:3, :])
print('array2d[:, :] \n', array2d[:, :])
print('array2d[:2, 1:] \n', array2d[:2, 1:])
print('array2d[:2, 0] \n', array2d[:2, 0])array2d:
[[1 2 3]
[4 5 6]
[7 8 9]]
array2d[0:2, 0:2]
[[1 2]
[4 5]]
array2d[1:3, 0:3]
[[4 5 6]
[7 8 9]]
array2d[1:3, :]
[[4 5 6]
[7 8 9]]
array2d[:, :]
[[1 2 3]
[4 5 6]
[7 8 9]]
array2d[:2, 1:]
[[2 3]
[5 6]]
array2d[:2, 0]
[1 4]

fancy indexing
array1d = np.arange(start=1, stop=10)
array2d = array1d.reshape(3,3)
array3 = array2d[[0,1], 2]
print('array2d[[0,1], 2] => ',array3.tolist())
array4 = array2d[[0,1], 0:2]
print('array2d[[0,1], 0:2] => ',array4.tolist())
array5 = array2d[[0,1]]
print('array2d[[0,1]] => ',array5.tolist())array2d[[0,1], 2] => [3, 6]
array2d[[0,1], 0:2] => [[1, 2], [4, 5]]
array2d[[0,1]] => [[1, 2, 3], [4, 5, 6]]


- Boolean indexing
array1d = np.arange(start=1, stop=10)
# [ ] 안에 array1d > 5 Boolean indexing을 적용
array3 = array1d[array1d > 5]
print('array1d > 5 불린 인덱싱 결과 값 :', array3)
array1d > 5array1d > 5 불린 인덱싱 결과 값 : [6 7 8 9]
array([False, False, False, False, False, True, True, True, True])


axis기반 matrix 정렬

선형대수 연산 – 행렬 내적과 전치 행렬 구하기
- 행렬 내적 : np.dot(A, B)
A = np.array([[1, 2, 3],
[4, 5, 6]])
B = np.array([[7, 8],
[9, 10],
[11, 12]])
dot_product = np.dot(A, B)
print('행렬 내적 결과:\n', dot_product)행렬 내적 결과:
[[ 58 64]
[139 154]]

- : 각각의 원소끼리 곱셈 (Elementwise product, Hadamard product)
@ : 행렬 곱셈 (Matrix product) <- dot product는 벡터개념 강조된 것. 이건 행렬 개념 강조
A = np.array( [[1,1],
[0,1]] )
B = np.array( [[2,0],
[3,4]] )
print(A * B)[[2 0]
[0 4]]
print(A @ B)
print(A.dot(B)) # 둘 다 결과는 동일하다.[[5 4]
[3 4]]
전치 행렬 : np.transpose(A)
A = np.array([[1, 2],
[3, 4]])
transpose_mat = np.transpose(A)
print('A의 전치 행렬:\n', transpose_mat)A의 전치 행렬:
[[1 3]
[2 4]]


행렬 연산
a = np.array( [20,30,40,50] )
print(a)
b = np.arange( 4 )
print(b)[20 30 40 50]
[0 1 2 3]
c = a-b # a에서 b에 각각의 원소를 -연산
print(c)[20 29 38 47]
# b 각각의 원소에 제곱 연산
print(b**2)[0 1 4 9]
# a 각각의 원소에 *10 연산
print(10*np.sin(a))[ 9.12945251 -9.88031624 7.4511316 -2.62374854]
# a 각각의 원소가 35보다 작은지 Boolean 결과
print(a<35)[ True True False False]
조건처리
- np.where( 조건, 조건이 True면 나올 값, else처럼 나머지 값)
ar = np.arange(9).reshape(3,3)
ararray([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
np.where(ar<4, -1, 999) # ar의 값이 4보다 작으면 -1, 나머지는 999로array([[ -1, -1, -1],
[ -1, 999, 999],
[999, 999, 999]])
np.where(ar<4, ar*10, ar-10) # 연산도 가능array([[ 0, 10, 20],
[30, -6, -5],
[-4, -3, -2]])
Addition
1차원
- append(값, 추가할 값)
a = np.arange(3)
np.append(a, [3,4,5]) # 기존에 3, 4, 5 추가
np.append(a, np.arange(3,6)) # 위와 아래 같은 결과array([0, 1, 2, 3, 4, 5])
np.append([3,4,5], a)
np.append(np.arange(3,6), a) # 앞에다가 추가array([3, 4, 5, 0, 1, 2])
- insert(값, 인덱스 위치, 추가할 값)
np.insert(a, 2, [101,102,103])array([ 0, 1, 101, 102, 103, 2])
2차원
- append(값, 추가할 값, 행렬선택) 행렬선택을 안하면 1차원으로 변형됨을 유의한다.
a_2d = np.arange(6).reshape(2,3)
a_2d_res = np.arange(6).reshape(2,3) * 5
np.append(a_2d, a_2d_res, axis=0) # axis=0 행으로 값 추가array([[ 0, 1, 2],
[ 3, 4, 5],
[ 0, 5, 10],
[15, 20, 25]])
a_2d의 2x3 mtx에 a_2d_res 라는 2x3 mtx가 밑으로 그대로 붙었다.
np.append(a_2d, a_2d_res, axis=1) # axis=1 열로 값 추가array([[ 0, 1, 2, 0, 5, 10],
[ 3, 4, 5, 15, 20, 25]])
추가 a_2d_res가 오른쪽으로 붙었다.
np.insert(a_2d, 1, 100, axis=0) # 인덱스 행이 1인 위치에 100으로 채워진 배열 추가array([[ 0, 1, 2],
[100, 100, 100],
[ 3, 4, 5]])
np.insert(a_2d, 1, 100, axis=1) # 인덱스 열이 1인 위치에 100으로 채워진 배열 추가array([[ 0, 100, 1, 2],
[ 3, 100, 4, 5]])
data = np.arange(100,103)
np.insert(a_2d, 1, data, axis = 0)array([[ 0, 1, 2],
[100, 101, 102],
[ 3, 4, 5]])
삭제
a_2d = np.arange(12).reshape(3,4)
a_2darray([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
np.delete(a_2d,1) # 1번 인덱스 원소만 삭제(1차원으로 변경)array([ 0, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
np.delete(a_2d,(0,1,3)) # 0번, 1번, 3번 인덱스 원소 여러개 삭제 가능(1차원으로 변경)array([ 2, 4, 5, 6, 7, 8, 9, 10, 11])
np.delete(a_2d, 0, axis=1) # col 삭제 (axis=0이면 row 삭제)array([[ 1, 2, 3],
[ 5, 6, 7],
[ 9, 10, 11]])
cloumn stack, vstack(vertical stack) 등 중요.
그외 병합, 분할 등이 있는데 그냥 ipynb파일이나 라이브러리 참조하자

'Programming > Python' 카테고리의 다른 글
| [ML] Logistic regression (0) | 2023.09.15 |
|---|---|
| [DL] tensorflow, Deep Neural Network(DNN) (0) | 2023.09.15 |
| [ML] Feature engineering, 다중회귀, 릿지회귀, 라쏘회귀 (1) | 2023.09.11 |
| [ML] KN 회귀 알고리즘, 선형회귀, 다항회귀 (0) | 2023.09.11 |
| [ML] KN 분류 알고리즘 (실전편) (0) | 2023.09.11 |



